Exercício:
Raquel Fernandes - Química Medicinal - 1º ano - Universidade da Beira Interior - Matemática - 2011/2012
quarta-feira, 8 de fevereiro de 2012
Problema de Cauchy
Equações Diferenciais
• Ordem: é dada pela ordem da maior derivada

• Grau: é dado pelo grau da derivada de maior ordem

Solução de uma EDO: é a função ou funções que satisfaz a equação diferencial:

Interpretação geométrica de uma EDO:
• Campo de direcções

Variáveis separáveis:


Exercícios:
1. Dada a seguinte taxa de crescimento, determine a taxa específica de crescimento.

segunda-feira, 6 de fevereiro de 2012
Exercícios sobre integração
domingo, 5 de fevereiro de 2012
Integral Indefinido
Integral Definido
Considere o problema de calcular a área da parte amarela do gráfico da função f (primeiro gráfico).
Podemos aproximar essa área - A - utilizando rectângulos: calcular a área por defeito (segundo gráfico) - Ai - ou calcular a área por excesso (terceiro gráfico) - As.
Logo, Ai < A < As.
Soma de Riemann:
Seja f uma função definida no intervalo [a,b]. O somatório abaixo descrito designa-se por Soma de Reimann
A Soma de Reimann pode ser usada para aproximar a área entre o gráfico de uma função e o eixo Ox no intervalo dado.
Definição de Integral Definido:
Seja f uma função contínua no intervalo [a,b]. Divida o intervalo em n subintervalos [Xi, Xi+1], sendo que X0 = a e Xn = b. Considere que ∆Xi = Xi+1 - Xi é o comprimento desse subintervalo. Tome qualquer valor Xi dentro desse subintervalo. Chamamos de integral definida de f de a até b o valor L tal que
Para simplificar a escrita utiliza-se
- O cálculo de uma área fica assim reduzido ao cálculo de uma primitiva.
Propriedades:
Teorema Fundamental do Cálculo:
Se f é contínua em [a,b], então  , sendo F uma antiderivada de f. Isto é, F'(x) = f(x).
, sendo F uma antiderivada de f. Isto é, F'(x) = f(x).
É comum representar F(b) - F(a) por 
- O Teorema Fundamental do Cálculo permite-nos calcular integrais definifos de uma maneira bem conveniente.
Antiderivada ou Integral
Definição: Uma função é denominada antiderivada ou primitiva de f sobre um intervalo I se F'(x)=f(x) para todo o x em I.
Teorema: Se F for uma antiderivada de f num intervalo I, então a antiderivada mais geral f em I é F(x)+C, onde C é uma constante arbitrária.
- Integrar é o contrário de derivar.
- A constante C só pode ser determinada se tivermos conhecimento do valor da integral em algum ponto específico. Cada função possui infinitas antiderivadas, diferenciadas entre si pelo valor específico de C.
Tabela de fórmulas de Antiderivação:
sábado, 4 de fevereiro de 2012
Polinómio de Taylor

- A principal propriedade deste polinómio é que ele passa pelo ponto (a; f(a)) e possui as mesmas derivadas até ordem n que a função f.
- O polinómio de Taylor de f desenvolvido numa vizinhaça de x=a aproxima a função nesta vizinhança.
Exercício:
1. Determine o polinómio de Taylor de grau 2 da função
 em torno do ponto x = 1.
em torno do ponto x = 1.Resolução:

A função pode ser simplificada.
Teorema do valor médio e teorema de Rolle
- f é contínua em [a,b]
- f é diferenciável em ]a,b[
 .
.Uma vez que f'(c) é a inclinação da recta tangente no ponto (c,f(c)), este teorema diz que há no mínimo ponto p (c, f(c)) sobre o gráfico onde a inclinação da recta tangente é igual à inclinação da recta secante AB.
Há um ponto p onde a recta tangente é paralela á recta secante AB.

Teorema de Rolle:
- f é contínua em [a,b]
- f é diferenciável em ]a,b[
- f(a) = f(b)

Regra de Cauchy ou Regra de L'Hôpital
Teste da 1ª e 2ª derivadas
- Monotonia de uma função:
Seja f(x) uma função contínua no intervalo [a,b] e diferenciável no intervalo ]a,b[.
- Se f ′(x) > 0 ∀x∈]a,b[, então f(x) é estritamente crescente em ]a,b[;
- Se f ′(x) < 0 ∀x∈]a,b[, então f(x) é estritamente decrescente em ]a,b[;
- Se f ′(x) = 0 ∀x∈]a,b[, então f(x) é constante em ]a,b[.
- Extremos de uma função:
- Uma função f tem um máximo absoluto em c se f(c) ≥ f(x) para todo o x pertencente ao domínio de f.
- Uma função f tem um mínimo absoluto em c se f(c) ≤ f(x) para todo o x pertencente ao domínio de f.
- Uma função f tem um máximo relativo em c se f(c) ≥ f(x) quando x estiver nas proximidades de c.
- Uma função f tem um mínimo relativo em c se f(c) ≤ f(x) quando x estiver próximo de c.
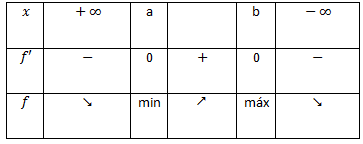
Como obter os extremos e estudar a monotonia de uma função:
- Calcular a derivada da função,
- Calcular os zeros da derivada,
- Construir um quadro de sinais.
a - minimizante
b - maximizante
f(a) - mínimo
f(b) - máximo
Teste da 2º derivada:
- Concavidade do gráfico de uma função
- Se f''(x) > 0 para todo o x em I, então o gráfico de f é côncavo para cima em I.
- Se f''(x) < 0 para todo o x em I, então o gráfico de f é côncavo para baixo em I.
p.i. - ponto de inflexão
Suponha que f'' seja contínua na proximidade de c:
- Se f'(x) = 0 e f''(x) > 0, então f tem um mínimo local em c.
- Se f'(x) = 0 e f''(x) < 0, então f tem um máximo local em c.
Derivadas
- A derivada num ponto é igual ao declive da recta tangente à função nesse ponto.
- A derivada é também chamada de taxa de variação instantânea ou velocidade.
Para calcular a derivada por definição num ponto recorre-se ao cálculo de um dos limites:
Derivadas laterais:
Só existe derivada num ponto se f'(x0) = f'(x0-) = f'(x0+)
Notas:
- Uma função pode ser contínua num ponto e não ter derivada nesse ponto. A continuidade não garante a derivabilidade.
- Toda a função que seja derivável num ponto x0 do seu domínio é contínua nesse ponto.
- Sempre que o gráfico de uma função f tiver um "pico" num ponto não tem derivada nesse mesmo ponto, uma vez que existem várias rectas tangentes (ex: f(x) = |x|).
- Dizemos que uma função é diferenciável se tiver derivada em todos os pontos do seu domínio.
- f'(x) = dy/dx = f^(1)(x).
Regras de diferenciação: