Teste da 1ª e 2ª derivadas

Teste da 1º derivada:

• Monotonia de uma função:

Seja f(x) uma função contínua no intervalo [a,b] e diferenciável no intervalo ]a,b[.

1. Se f ′(x) > 0 ∀x∈]a,b[, então f(x) é estritamente crescente em ]a,b[;
2. Se f ′(x) < 0 ∀x∈]a,b[, então f(x) é estritamente decrescente em ]a,b[;
3. Se f ′(x) = 0 ∀x∈]a,b[, então f(x) é constante em ]a,b[.

• Extremos de uma função:

1. Uma função f tem um máximo absoluto em c se f(c) ≥ f(x) para todo o x pertencente ao domínio de f.
2. Uma função f tem um mínimo absoluto em c se f(c) ≤ f(x) para todo o x pertencente ao domínio de f.
3. Uma função f tem um máximo relativo em c se f(c) ≥ f(x) quando x estiver nas proximidades de c.
4. Uma função f tem um mínimo relativo em c se f(c) ≤ f(x) quando x estiver próximo de c.

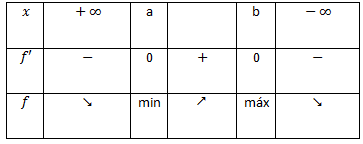
Como obter os extremos e estudar a monotonia de uma função:

1. Calcular a derivada da função,
2. Calcular os zeros da derivada,
3. Construir um quadro de sinais.

a - minimizante

b - maximizante

f(a) - mínimo

f(b) - máximo

Teste da 2º derivada:

• Concavidade do gráfico de uma função

1. Se f''(x) > 0 para todo o x em I, então o gráfico de f é côncavo para cima em I.
2. Se f''(x) < 0 para todo o x em I, então o gráfico de f é côncavo para baixo em I.

p.i. - ponto de inflexão

Suponha que f'' seja contínua na proximidade de c:

1. Se f'(x) = 0 e f''(x) > 0, então f tem um mínimo local em c.
2. Se f'(x) = 0 e f''(x) < 0, então f tem um máximo local em c.